前端如何实现模糊搜索
前端如何实现模糊搜索
模糊搜索大家在日常开发中应该经常接触。一般来说,模糊搜索多由后端完成。但是如果数据量只有几十条或者几百条,用后端进行模糊搜索明显会增加http请求的压力。这时候,前端模糊搜索就派上用场了。前端模糊搜索主要针对数据量相对较少,数据变动相对较小的结果。后端一次性返回所有数据,前端根据已有数据进行模糊搜索,并将最理想的结果返回给用户。
前端模糊搜索的核心算法是最短编辑距离算法。什么是最短编辑距离?简单来说,最短编辑距离就是从字符串A变成字符串B需要进行几步操作。这其中涉及到了字符的增、删、改三种操作。下面我们来具体介绍下算法原理和实现。
算法简介
最短编辑距离算法,又叫Levenshitein距离算法。是由俄罗斯数学家Vladimir Levenshtein在1965年提出的。是指字符串A转换成字符串B所需的最少操作。其中包括的操作有:
- 删除一个字符
- 插入一个字符
- 修改一个字符
一般来说,两个字符串的编辑距离越短,则这两个字符越相似。如果两个字符串相等,则它们的编辑距离为0。不难看出,两个字符串的编辑距离肯定不会超过字符串的最大长度。
创建动态规划方程
最短编辑距离算法通过将两个字符串拆分成字符,然后进行逐一比较并获得相应的值,最终得到最短编辑距离,这里我们使用矩阵表示。下面我们来对矩阵进行分析,首先我们定义[V0, H0]为0,对应的行和列依次递增。生成的默认矩阵如下:
| H0 | H1 | H2 | H3 | H4 | H5 | H6 | H7 | ||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 质 | 量 | 保 | 证 | 金 | 总 | 额 | ||
| V0 | 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| V1 | 固 | 1 | |||||||
| V2 | 定 | 2 | |||||||
| V3 | 租 | 3 | |||||||
| V4 | 金 | 4 | |||||||
| V5 | 总 | 5 | |||||||
| V6 | 额 | 6 |
下面我们来为空白处填充最短编辑距离(这里我们是要把固定租金总额转换成质量保证金总额)。首先,我们计算 [V1, H1] 的值,V1 对应的字符是 固,V1 对应的字符是 质,显然 V1 !== H1,所以他们的变换需要做修改(flag为1)。这时候,我们通过增、删、改的操作,计算得到 [V1, H0] + 1、[V0, H1] + 1、[V0, H0] + flag 中的最小值就是当前字符的最短编辑距离,并填入 [V1, H1] 空白处。以此类推,计算出最终的 [Vn, Hm] 就是最短编辑距离。计算公式为 min([Vx, Hy - 1] + 1, [Vx - 1, Hy] + 1, [Vx - 1, Hy - 1] + flag)。
flag的值与Vx和Hy的比较结果有关。如果Vx === Hy,flag为 0,否则flag为 1。Vn和Hm中的n和m指最后一个字符的坐标值。Vx和Hy中的x和y指当前正在计算的字符的坐标值。
| H0 | H1 | H2 | H3 | H4 | H5 | H6 | H7 | ||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 质 | 量 | 保 | 证 | 金 | 总 | 额 | ||
| V0 | 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| V1 | 固 | 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| V2 | 定 | 2 | 2 | 2 | 3 | 4 | 5 | 6 | 7 |
| V3 | 租 | 3 | 3 | 3 | 3 | 4 | 5 | 6 | 7 |
| V4 | 金 | 4 | 4 | 4 | 4 | 4 | 4 | 5 | 6 |
| V5 | 总 | 5 | 5 | 5 | 5 | 5 | 5 | 4 | 5 |
| V6 | 额 | 6 | 6 | 6 | 6 | 6 | 6 | 5 | 4 |
最终计算所得,上面的两个字符串的 最短编辑距离为4。
从上面的分析,我们不难推导出动态规划方程:
代码实现与优化
理解了理论知识,代码实现上其实非常简单。无非就是字符的比较,以及对字符的增、删、改操作,得到的矩阵最末尾的数字就是最短编辑距离。具体算法如下:
/**
* 编辑距离算法(LD algorithm)
* @param {string} source 输入的内容
* @param {string} target 匹配的目标
* @return {number}
*/
function levensheinDistance (source, target) {
const sourceLength = source.length
const targetLength = target.length
const space = new Array(targetLength)
// 过滤目标或者比较值为空字符串的情况
if (sourceLength === 0) {
return targetLength
} else if (targetLength === 0) {
return sourceLength
} else {
for (let i = 0; i < sourceLength; i++) {
const sourceChar = source[i]
let temp = i
for (let j = 0; j < targetLength; j++) {
const targetChar = target[j]
// 获取前一个数值
const prevDistance = j === 0 ? i + 1 : space[j - 1]
// 获取上一个数值
const topDistance = space[j] === undefined ? j + 1 : space[j]
// 判断是否需要修改
const flag = sourceChar === targetChar ? 0 : 1
// 获取增,删,改和不变得到的最小值
const min = Math.min(prevDistance + 1, topDistance + 1, temp + flag)
// 保存左上角的数据,计算最小值时需要用到
temp = topDistance
space[j] = min
}
}
// 获取数组的最后一位,即编辑距离
return space[targetLength - 1]
}
}以上就是算法实现的全部内容。算法本身很简单,这里对空间复杂度做了优化,使用一维数组来表示矩阵。
m是指上面矩阵Hm中的m,这里代表的是target.length。n是指上面矩阵Vn中的n,这里代表的是source.length。
首先,我们创建了一个m长度的数组(space)。
内循环:
temp保存的是 [Vx-1, Hy-1]。prevDistance保存的是 [Vx-1, Hy]。topDistance保存的是 [Vx, Hy-1]。
- 通过判断
sourceChar与targetChar是否相同,得出结论flag的值。 - 计算到当前字符为止的最小编辑距离是多少。
- 将
topDistance赋值给temp,因为在下一个循环中这个值将作为 [Vx-1, Hy-1] 出现。 - 更新 [Vx, Hy] 的值。
- 循环往复,直到两层遍历都完成为止。
从这里我们可以看到,space是一个非常特殊的一维数组。它首先会保存 Vx-1 层的最短编辑距离,在内循环不断执行过程中,Vx-1 层的最短编辑距离会被 Vx 层的最短编辑距离逐步替换。如此往复,当循环结束时,space[target.length - 1]即是 [Vx, Hy]。
在模糊搜索中的应用
讲到这里,我们已经实现了模糊搜索的核心部分。我们只需要获得 相似度【distance / Math.max(A.length, B.length)】,然后进行 过滤,排序 操作,即可实现比较完美的模糊搜索功能。
由于相似度只跟最大字符长度和编辑距离有关,这样还是会存在期望的内容无法尽早的出现在前几位。那搜索的结果是否还能更精确些呢? 答案当然是肯定的。我认为因子越多,得到的模糊匹配的结果就越趋于期望结果。所以在模糊搜索中,我添加了最大连续匹配长度、匹配个数、首个匹配字母位置等因子,最后通过复杂的计算和权重的配比得到期望的结果。
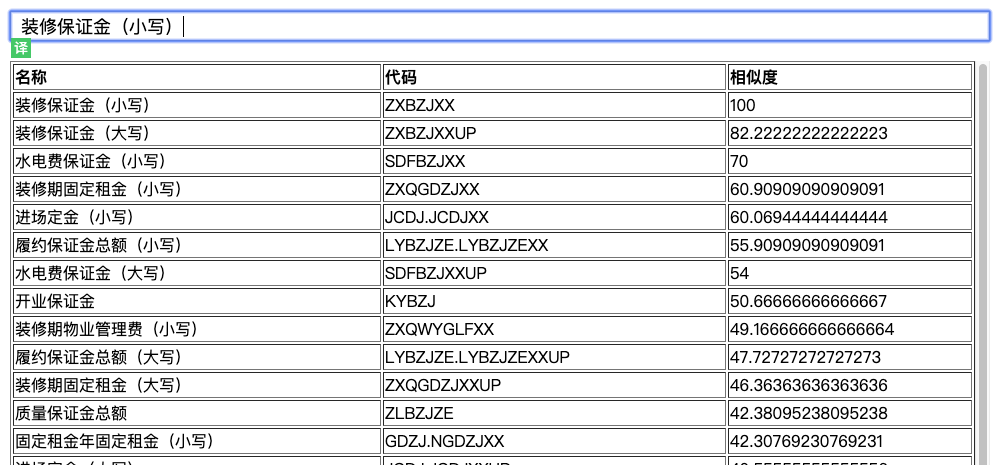
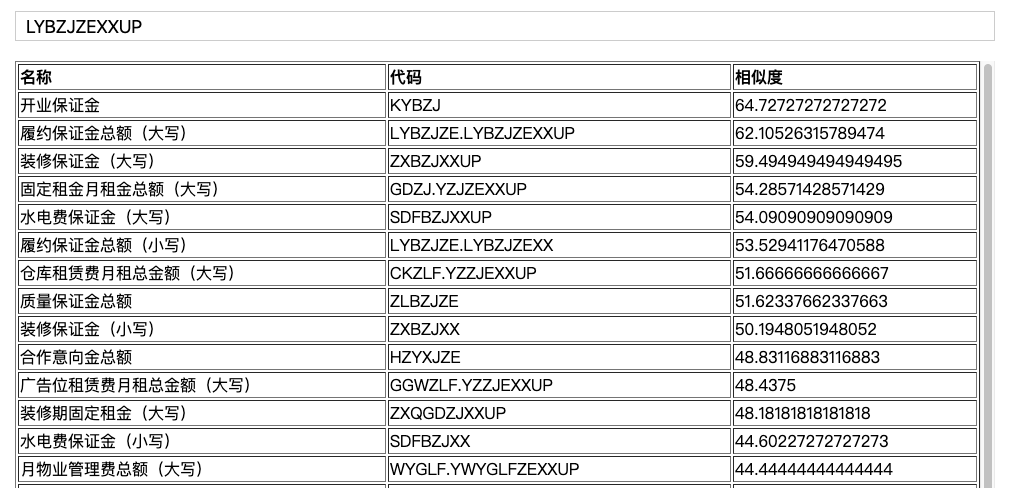
在代码实现上,需要在 最短编辑距离算法 中混入一些关键节点的计算,获得想要的因子。
无论如何变化,模糊搜索的核心仍然是基于 最短编辑距离算法 完成的。您也可以根据您的想法,添加更多的因子,订制一套自己的模糊搜索。
结论
动手编写一个模糊搜索确实不算太难。只要掌握 最短编辑距离算法 的思想,围绕这个算法添加一些自己想要的因子,然后通过权重配置和复杂的计算公式得到相似度,最后过滤、排序、输出结果即可。无论如何,最短编辑距离算法才是模糊搜索的核心。
题外话
这里是我实现的模糊搜索方法,您可以作为学习和参考。